Hai sobat Belajar MTK – Untuk Kalian yang duduk di kelas XII, pembahasan tentang rumus pencerminan terhadap garis y=-x dan contoh soalnya tentu sangat dibutuhkan untuk memahami materi ini. Pencerminan atau refleksi merupakan salah satu jenis transformasi geometri selain translasi (pergeseran), rotasi (perputaran), dan dilatasi (perkalian). Apa pengertian dari keempat jenis transformasi tersebut dapat Kalian simak di bawah ini.
A. Konsep Pencerminan (Refleksi)
Transformasi geometri dicetuskan pertama kali oleh seorang matematikawan bernama Felix Klein. Menurutnya, sebuah bangun geometri bisa diubah letak, bentuk, atau ukurannya, baik yang berbentuk segitiga, lingkaran, persegi, limas, maupun bentuk lainnya.
Seperti Kalian ketahui, bangun ruang terbentuk dari kumpulan garis-garis yang dihubungkan secara sistematis. Sementara itu, garis sendiri adalah kumpulan titik-titik yang dihubungkan secara sistematis. Karena itu, transformasi geometri tidak hanya bisa terjadi pada bangun ruang, tetapi berlaku juga untuk titik dan garis.
Transformasi atau perubahan yang terjadi pada bangun geometri terjadi melalui empat cara, yaitu pergeseran, perputaran, pencerminan, dan perbesaran/pengecilan atau perkalian. Namun, pada tulisan kali ini, kita akan membahas salah satunya, yaitu pencerminan atau refleksi, khususnya rumus pencerminan terhadap garis y=-x.
Untuk memahami konsep tentang pencerminan, perhatikan gambar berikut.

Kalian tentu tidak merasa asing lagi melihat gambar di atas, bukan? Ya, konsep pencerminan sebenarnya sangat mudah dipahami karena dalam kehidupan sehari-hari, Kalian juga pasti sering bercermin. Dari gambar di atas, Kalian bisa melihat bahwa refleksi atau pencerminan memiliki sifat-sifat khas, yaitu:
- Objek dan bayangannya selalu sama baik bentuk maupun ukurannya.
- Jarak setiap titik pada objek ke cermin sama dengan jarak antara setiap titik pada bayangan ke cermin (s=s’)
- Tinggi objek dan tinggi bayangan adalah sama (h=h’)
- Garis yang menghubungkan titik pada objek dengan titik pada bayangan selalu tegak lurus terhadap cermin.
Nah, sekarang, coba perhatikan gambar berikut ini.

Berdasarkan sifat-sifat pencerminan di atas, bisa disimpulkan bahwa:
- Segitiga PQR kongruen dengan segitiga P’Q’R’ sehingga luas kedua segitiga tersebut juga sama.
- RA=R’A, PB=P’B, dan QC=Q’C. Dengan kata lain, jarak titik sudut segitiga PQR ke cermin sama dengan jarak titik sudut P’Q’R’ ke cermin.
- Tinggi segitiga PQR sama dengan tinggi P’Q’R’.
- Ruas garis PP’, QQ’, dan RR’ tegak lurus terhadap cermin (garis AC)
B. Rumus Pencerminan terhadap Garis y=-x
Setelah memahami konsep dan sifat-sifat pencerminan, sekarang kita masuk pada pembahasan rumus pencerminan terhadap garis y=-x dan contoh soalnya. Pada koordinat kartesius, sebuah titik atau persamaan dapat ditransformasikan secara geometri, salah satunya melalui pencerminan.
Pencerminan terhadap garis y=-x pada dasarnya akan mengubah posisi objek pada koordinat kartesius dengan cara mencerminkan objek tersebut terhadap garis y=-x. Untuk memudahkan Kalian dalam memahaminya, perhatikan gambar berikut ini.

Pada gambar terlihat titik P dengan koordinat (x,y) yang dicerminkan terhadap garis y=-x. Hasil bayangan titik P adalah titik P’ dengan koordinat (-y,-x). Jika dituliskan dalam bentuk matriks, matriks transformasi pencerminan terhadap garis y=-x adalah:

Dengan demikian, matriks bayangan hasil transformasinya adalah sebagai berikut:

Matriks transformasi tersebut berlaku untuk koordinat sebuah titik maupun persamaan garis/kurva dengan hasil pencerminan sebagai berikut:
- Bayangan hasil refleksi sebuah titik:
A(x,y) —> A'(-y,-x)
- Bayangan hasil refleksi sebuah garis:
y=f(x) —> x=-f(-y)
Nah, rumus pencerminan terhadap garis y=-x sudah Kalian ketahui. Sekarang, Kalian bisa mempelajari contoh soal dan pembahasannya berikut ini agar lebih memahami materi pencerminan ini.
C. Contoh Soal
- Soal 1
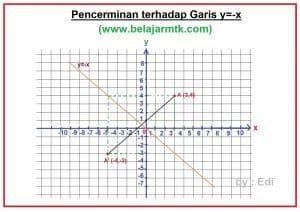
Diketahui titik A terletak pada koordinat (3, 4). Tentukan koordinat bayangan titik A jika direfleksikan terhadap garis y=-x.
Pembahasan:
Dengan menggunakan rumus A(x,y) —> A'(-y,-x), koordinat titik A’ (hasil pencerminan terhadap garis y=-x) adalah:
x’ = -y
x’ = -4
y’ =-x
y’ =-3
Jadi, koordinat A’ adalah (-4,-3).
- Soal 2
Diketahui titik A terletak pada koordinat (-2, 5). Tentukan koordinat bayangan titik A jika direfleksikan terhadap garis y=-x.
Pembahasan:
Dengan menggunakan rumus A(x,y) —> A'(-y,-x), koordinat titik A’ (hasil pencerminan terhadap garis y=-x) adalah:
x’ = -y
x’ = -5
y’ =-(-2)
y’ =2
Jadi, koordinat A’ adalah (-5, 2).
- Soal 3
Tentukan bayangan garis yang memiliki persamaan y=3x+8 terhadap garis y=-x.
Pembahasan:
Berdasarkan matriks transformasi, maka x’=-y dan y’=-x.
Jika x’ dan y’ disubstitusikan ke dalam persamaan asalnya, akan diperoleh:
y’=3x’+8
-x=3(-y)+8
-x=-3x+8
x=3y-8
Baca juga : Pencerminan Terhadap Garis x=h dan y=k Beserta Contohnya
Itulah penjelasan tentang rumus pencerminan terhadap garis y=-x dan contoh soalnya Sudah cukup jelas, bukan? Agar makin mahir dan memahami materi ini, sering-seringlah berlatih mengerjakan soal.
Berikut kalkulator rumus pencerminan terhadap Garis y=-x, silahkan dicoba

sangat membantu!