Hai sobat Belajar MTK – Dalam artikel kali ini kita akan membahas tentang rumus pergeseran translasi dan contoh soalnya untuk membantu para siswa memahami materi tersebut. Translasi atau pergeseran termasuk ke dalam materi pelajaran matematika tentang transformasi geometri. Ada beberapa jenis yang termasuk ke dalam bab transformasi geometri ini selain translasi.
Secara umum terdapat 4 jenis transformasi dalam matematika geometri tersebut. Meskipun pada tulisan ini hanya akan dibahas tentang translasi saja tetapi tidak ada salahnya jika siswa juga mengetahui sekilas mengenai jenis lainnya. Dengan mengetahui semua jenis transformasi geometri yang ada diharapkan nantinya para siswa akan lebih mudah memahami pembahasannya.
Sebagai pengantar atau pendahuluan sebelum memasuki pembahasan tentang translasi, silahkan simak dulu beberapa poin penting berikut ini.
A. Jenis Transformasi Geometri dalam Matematika
1. Translasi atau Pergeseran
Pengertian dari translasi atau pergeseran yaitu jenis transformasi atau pergeseran titik yang terjadi di sepanjang garis yang lurus dengan arah serta jarak. Proses translasi atau pergeseran tersebut hanya akan memindahkan titik saja. Sedangkan untuk menentukan hasil obyek yang mengalami translasi tidaklah sulit. Caranya yaitu menambahkan absis dan ordinat pada jarak tertentu sesuai dengan rumus.

2. Refleksi atau Pencerminan
Refleksi adalah jenis transformasi dengan memindahkan titik pada bidang datar dengan mempergunakan sifat seperti yang terjadi pada bayangan cermin datar. Hasil dari pencerminan nantinya tergantung dari jenis sumbu yang menjadi cermin titik tersebut.
3. Rotasi atau Perputaran
Rotasi yaitu transformasi dimana terjadi perubahan posisi pada obyek dengan cara diputar dari suatu sudut tertentu. Besaran rotasi sesuai dengan rumus ada 2 jenis yaitu :
- a untuk rotasi yang dilakukan berlawanan dengan arah jarum jam
- – a untuk rotasi yang dilakukan searah dengan jarum jam
Hasil perhitungan dari rotasi akan tergantung pada besarnya sudut yang digunakan.
4. Dilatasi atau Perkalian
Pengertian dari dilatasi adalah transformasi yang akan merubah ukuran benda. Hal tersebut dikarenakan dalam dilatasi benda akan mengalami perbesaran atau pengecilan obyek. Dilatasi agak berbeda dengan jenis transformasi lainnya karena tidak merubah ukuran melainkan hanya merubah posisinya saja.
Setelah mengetahui secara singkat tentang jenis tranformasi geometri selanjutnya akan kita bahas khusus tentang rumus pergeseran translasi dan contoh soalnya.
B. Rumus Translasi Beserta Contohnya
Rumus Translasi atau Pergeseran
Seperti pada jenis transformasi geometri yang lainnya, translasi juga mempunyai sebuah rumus tertentu. Rumus dari translasi yaitu :
T [a,b]
A (x,y) ———> A'( x’ , y’)
Rumus Translasi
T [a,b]
A (x,y) ———> A'( x + a , y+ b)
Keterangan :
- (x, y ) adalah asal titik yang digeser
- (x’, y’ ) adalah titik dari bayangan
- (a, b ) adalah vektor translasi
Contoh Soal :
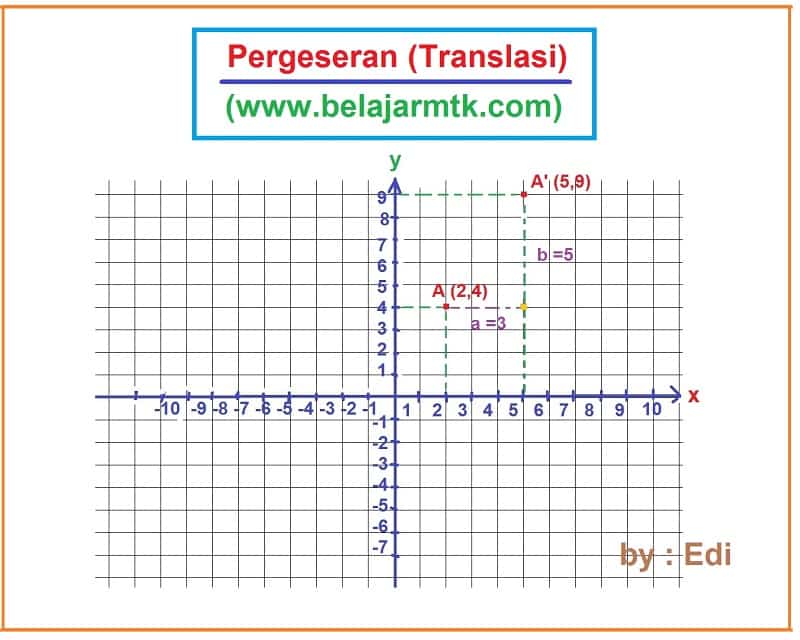
Tentukan bayangan dari titik A (2,4) pada translasi (3,5)
Jawaban dan pembahasan :
Untuk menjawab soal yang diberikan di atas dengan cara yang lebih mudah masukkan dulu semua angka sesuai dengan keterangan pada rumusnya.
Ingat rumus untuk mengetahui hasil translasi adalah A (x,y) ———> A'( x + a , y+ b)
Pembahasan soal :
- Berapakah hasil dari A'(x’, y’) sesuai dengan soal di atas?
- Masukkan semua angka sesuai rumus yaitu : (x,y) = (2,4) ; (a,b) = (3,5)
- Lalu hitung hasilnya sesuai rumus yaitu :
A’ (x’,y’) = {(x+a), (y+b)}
A’ (x’,y’) = {(2+3), (4+5)}
A’ (x’,y’) = (5,9)
- Jawaban soal :
Dari hasil perhitungan soal translasi di atas sesuai dengan rumus yang ada didapatkan jawaban A'(x’,y’) = (5,9). Gunakan cara yang sama ketika ada latihan soal dengan angka yang berbeda.
Tahapannya juga sama yaitu masukkan titik bayangan dan vektor translasi sesuai tempat masing-masing seperti pada rumusnya. Menggunakan cara seperti itu akan memudahkan siswa mendapatkan hasil translasi dari sebuah titik.
Baca juga : Pencerminan Terhadap Garis x=h dan y=k
Itulah pembahasan singkat dari materi rumus pergeseran translasi dan contoh soalnya yang merupakan bagian dari transformasi geometri. Diharapkan setelah ini siswa lebih memahami dan bisa menyelesaikan soal yang diberikan.
Berikut kalkulator rumus pergeseran atau translasi, silahkan dicoba.